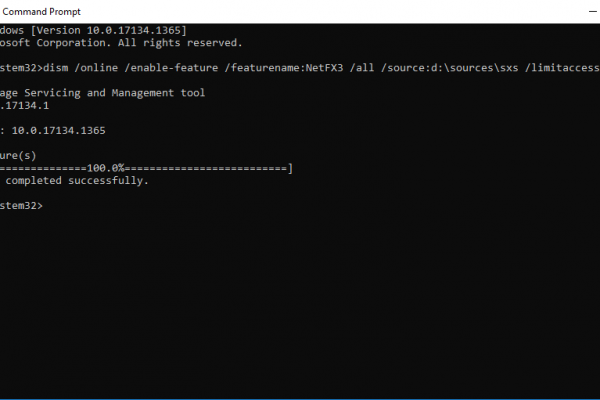
I’ve come across this issue several times where an application depends on .Net Framework 3.5. For some, this can either take a lot of time …
Category: Windows 10
Windows 10 has some scrollbars as part of it’s UI that can shrink and disappear. This can cause some frustration for some users that don’t …
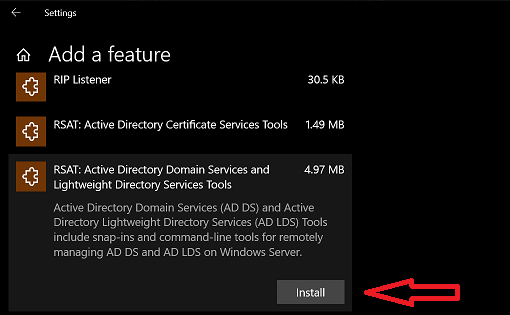
For many Windows administrators that want to connect to a domain controller from a Windows 10 client machine, they like to use Microsoft’s Remote Server …
Some folders in File Explorer will default to grouping by what time period the file was accessed. Many people do not like this style of …
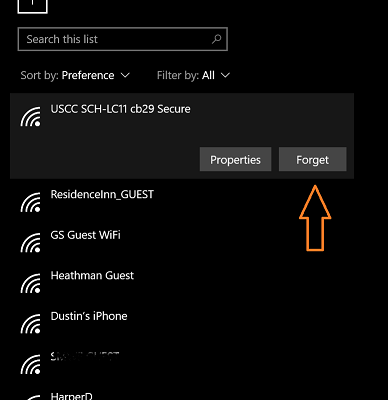
Every so often, it makes good sense to go into your network settings and forget some of the networks you have connected to previously. This …
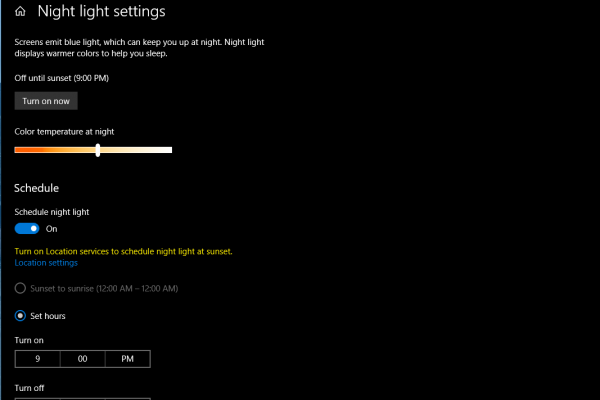
Windows 10 introduced a new feature that allows you to limit the blue light at a certain time to help with sleep patterns and to …
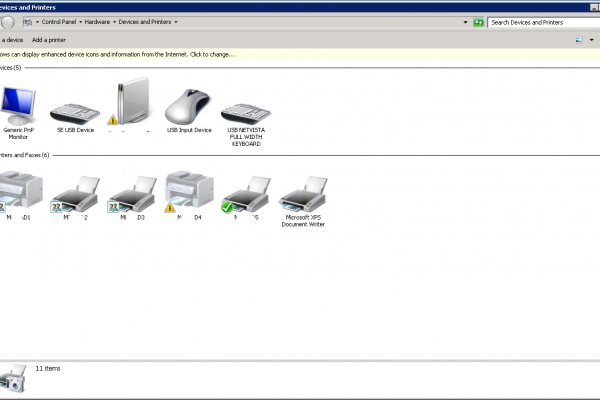
Sometimes, network printers can show as offline yet still be functional. This is due to recent versions of Windows Server and clients using SNMP for …
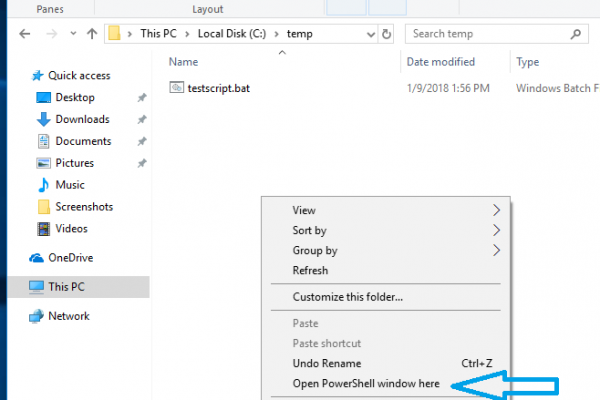
Many times, you are browsing folders and find a console style program that you’d like to run, but would like to do it from the …
Manipulating windows within Windows 10 is pretty simple. If you have multiple windows open and you want to make things easier to read, or to …
Windows 10 was supposed to be the last version of Windows. It really is in a way. However, rather than incrementing the version number itself, …